東京・神奈川・埼玉・千葉・茨城　中学受験情報

前回は、偏差値が模試受験生のなかでの得点の分布状態を反映させた相対的位置をあらわす指標であること、また出題レベルや母集団のレベルが異なる模試では出てくる「偏差値」も大きく変わることがあるという話をしました。今回は「偏差値」による志望校の合否判定にまつわる話および「偏差値」の上手な活用法についてお話をします。

3.「偏差値」による合否判定についてのいくつかの問題

各模試における「偏差値」による志望校の合否判定は学校ごとの「合格基準偏差値」によって行われます。「合格基準偏差値」は前年度入試の「結果偏差値」をベースにして決めますが、「結果偏差値」を出すための作業は、まず前年の模試受験生の実際の入試結果の追跡調査から始まります。

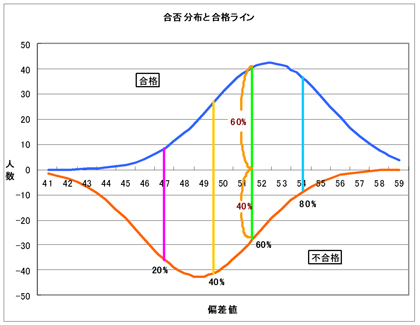
集まったデータはすべて入力され、学校・入試回ごとに合否別の度数分布表（およびグラフ）を作成し偏差値ごとの合格者と不合格者の人数（割合）から、合格率80％、60％、40％・・・となる偏差値を読み取って「結果偏差値」を決めていき（実際には欠落している部分を推測して補いながら読んでいきます。）、4月中には各模試会社から「○○年度中学入試結果偏差値（△△社版）」として公表されます。

この時期になると週刊誌や経済誌などで「今春入試で注目の中学」とか「今年大きく偏差値を上げた中学」などという記事が出ますが、これは各社から出された「結果偏差値」にもとづいています。

では翌年の入試の合否判定の「合格基準偏差値」にこの「結果偏差値」がそのまま使われるかと言えばそうではありません。次年度の募集要項（募集定員、試験日、試験科目など）が夏休みまでに各中学から続々と発表され、9月初旬までにはほとんどが出ます。

次年度の合格基準偏差値はこの募集要項、あるいは他校との競合関係、難化または易化に対する反動要因、大学合格実績、学校改革に対する評価などに注目して「結果偏差値」をベースにしながらこれに総合的見地から変動を予想したものが「予想偏差値」になります。そしてこの「予想偏差値」が各模試会社の合否判定のプログラムのなかで「合格基準偏差値」として使われるわけです。

こうして決まった「合格基準偏差値」に基づいて合否判定が行われるのですが、当然ながら完全無欠であるわけではありません。以下にいくつかの具体的な問題点をあげてみます。

1. 追跡調査の問題
   前年の模試の受験生の本番入試の結果の追跡調査の回収率（判明率）は中位・下位校になるほど低くなる傾向があるようです。中・下位層になるとどうしても合格率が下がり、とくに下位層では不本意な学校しか受からなかったり全滅したりするケースがでてきます。
   
   このような場合、受験生とその家族が模試会社の追跡調査に協力する気になれないのは無理もありません。合格校だけ回答するというケースもかなりあるようです。下位校はそもそも受験者が少ない学校が多く、当然データ件数が少ないのですが、そのうえ不合格データが集まらないと合格可能性ラインを読み取ることができなくなります。データ件数の少ない学校では、かなりの推定を交えて合格基準値を決めざるを得ないのが実情です。
   
   ※中下位校のなかでは人気のあるＭ女子学院の今年の第1回入試では175人が受験し149人が合格しました（補欠合格3人含む）。この学校についての、ある模試の追跡調査データは71件ありますが、すべて合格データです。26人の不合格者のデータは1件も回収されていないために、これだけで見ると偏差値28から58まで誰でも合格するように見えてしまいます。データに忠実なのが科学的とは限らないケースです。
2. 合否分布の問題
   学校によっては合否の分布がきれいなグラフにならない場合があります。普通に考えて偏差値が高ければ合格率は高く、偏差値が低ければ合格率は低くなるはずですが、実際の入試データではかなり高い偏差値で不合格が目立っていたり、逆に低めの偏差値でけっこう合格者がいたりして、非常に合格ラインが読みにくい場合があります。
   
   こうなる理由としては追跡調査の回収率が低く例外的なデータばかり拾ってしまっている場合もありますが、入試問題にくせがあって合否に乱高下が生ずる場合、志望順位が低いため過去問にしっかり取り組んでいなかった場合、受験生の偏差値に前回述べたような大きな変動があった場合、あるいは学力試験以外の要素（面接など）が合否判定に大きく影響している場合などが考えられます。
   
   また合格者と不合格者の重なっている偏差値帯がずっと広がっていて、その間では合否がほとんど相半ばしている分布などでは合格率60％、40％などをどこで線引きすればよいのか苦慮することになります。
   
   ※通常、「K大付属中の偏差値は65だ。」などというときの偏差値は合格率80％ラインの数字で表すことが多いようですが、合格率80％ラインが同じでも60％、40％ラインまで下げてみると大きく異なる場合、入試の実態は全く異なると考えられます。40％ラインや20％ラインが下まで広がっている学校は志望順位の高い他校との併願者が多く、合格者を非常に多く出しているため、形式倍率が非常に高くとも実質倍率は低く、合格点も低くなっている学校が多いようです。
   
   ※「合格基準偏差値」はあくまで入試の合格可能性の目安であって、その学校の教育に対する評価とは全く別のものですが、さらに言えば学校の学力レベルでもありません。学校の学力レベルを偏差値で表すならば「入学者平均偏差値」を用いるのが最も妥当です。たとえばある模試のデータによれば、P大中とQ大中は共に80％ライン偏差値が54ですが、「入学者平均偏差値」では前者が47．7で後者が49．5と2ポイント近くQ大中のほうが高くなっています。
3. 複数回受験
   最近は複数回受験者に対する優遇措置をとる学校が増えているため後半日程の入試で低い偏差値の合格データの目立つ学校があります。このような場合、「合格基準偏差値」は優遇を受けて合格した受験生のデータが含まれるため偏差値が低く設定されるので、次のようなケースも起こりうるので注意が必要です。

――― よう子さんは第一志望のＲ女学院を受け、1回目は全く届かず、2回目は優遇を受けたのですが僅かに届かず、ようやく3回目にぎりぎりでしたがめでたく合格できました。

よう子さんと仲良しのみどりさんは前半日程でより高いレベルの学校を受けて不合格となり初めてＲ女学院の3回目をよう子さんと一緒に受験。初受験ですから優遇措置を受けることはできません。

そんなこととは知らず、みどりさんが「自分の偏差値なら楽勝のはず！」と思いながら合格発表を見ると、よう子さんの受験番号はあるのに自分の番号がない。「いつの模試でも私のほうが偏差値高かったのに！（涙、涙・・）」 ―――

もちろんこれは架空の話ですが、入試の仕組みをよく知らずに偏差値だけで入試を判断するとこんな事だってあるかもしれません。なおこの場合、R女学院の3回目に低めの偏差値をつけた模試会社に落ち度があるわけではないでしょう。

4.「偏差値」による合否判定の見方

受験生・保護者にとって志望校の合格可能性の見通しを考えるとき、模試の合否判定は大きな拠り所です。しかし、よく言われるように「偏差値」は目安に過ぎないですし、全くの見当違いではないとしても「判定」を100％信頼できるわけではありません。

何回かの模試を受ければ受験生の各回の「偏差値」自体に少なくとも±3程度の幅があるのが普通だと見てよいでしょう。その理由は本人の学力の上昇・停滞・下降以外にも（2）で述べたような模試自体に起因する場合もあります。したがって受験者数、平均点、さらに可能なら標準偏差などをチェックして各回の模試の全体的な状況は把握しておいた方がよいでしょう。

また各学校の「合格基準偏差値」にも（3）で述べたような問題があり、学校にもよりますが判定基準にも幅があることを理解した上で見ていくことにより、合格可能性についてもより立体的な見方ができるようになるでしょう。

特に中学入試では問題との相性に左右されることも多いので、合格の可能性を見極めるためには、模試の判定と同時に受験校の過去問に取り組んだときの手応えと合わせて、複眼的に見ていくことをお勧めします。

最後に「偏差値」の活用法についてのご提案です！

1. 受験生の持ち点ともいうべき「偏差値」は幅があります。その幅は少なくとも±2～3、大きければ±5程度です。それを考える際には本人の調子や各模試の状況も考慮した方がよいでしょう。
2. 学校の「偏差値」にも幅をみてください。合格率80％、60％・・・のラインの幅は学校によってかなり異なります。他校との併願受験者の多い学校ではかなり下でも合格の可能性が結構あります。
3. 受験生の「偏差値帯」と学校の「偏差値帯」にわずかでも重なりがあればチャレンジの価値はあります。しかしまったく重なりがないのであれば無謀な受験ということになります。（いわゆるあこがれ受験です。）
4. 受験生の「偏差値帯」の下限が学校の「偏差値帯」の60％ラインより下にはみ出していれば、安全校としてはかなりのリスクがあると考えるべきです。安全校を選ぶなら、受験生の「偏差値帯」が学校の「偏差値帯」の20％ラインより上に収まる学校にすべきでしょう。