東京・神奈川・埼玉・千葉・茨城　中学受験情報

今回は「偏差値」についての話です。特に中学受験を目指している小6生の保護者にとってこの時期に「偏差値の話」というとシビアな内容の話を予想するかもしれませんが、今回は「偏差値」にまつわるいくつかのエピソードと、「偏差値」の見方、使い方の話をしてみたいと思います。

1.そもそも「偏差値」ってなに？

「うちの子は偏差値が低くって受かりそうな学校ないわ」とか「おとなりのさやかちゃんの受かった○○女子中学って偏差値高いらしいわよ」などという日常的な会話、あるいは比喩的な使い方としては「美人（イケメン）偏差値」、「オタク偏差値」などいくらでも使えそうな「偏差値」という言葉、ご存じと思いますが実は数学の一分野である統計学の手法によって求められる統計量です。

ところで「偏差値 standard score」という言葉が日常会話のなかでも普通に使われているのは世界中で日本だけです。なぜかと言えば日本だけで「偏差値」が中学受験、高校受験、大学受験の模試で学力の評価方法として広い範囲で一般的に使われているからです。ではなぜ「偏差値」が学力の評価方法として使われるようになったのでしょう。

日本で成績評価に初めて統計的手法（現在の偏差値の前身）を使ったのは塾でも学校でもなく、なんと旧陸軍でした。大砲の射撃訓練で砲兵に成績をつけるときに単純な点数ではなく統計的手法を応用したのが事の始まりだったそうです。時が過ぎて戦後になり日本が高度成長期をむかえ、生徒が急増するとともに、高校進学率も急上昇し高校受験がまさに受験戦争の様相を呈してきたとき（団塊の世代が高校受験のころです）に、都内の公立中学校のある先生によってより精度の高い進路指導のために、いくつかの工夫を加えて現在使われている形の「偏差値」が使われるようになったのです。

さて模試の場合の「偏差値」は、個々の受験生がその回の受験者全体の集団（母集団）の中でどのような位置（相対的位置））にいるかを表したものです。

母集団のなかでの相対的位置を知る方法としては「何人中何番」とか「平均点より何点上」などの素朴な表し方もありますが、このような方法では得点の分布状態の差異を反映させた評価をすることができません。たとえば明男君がテストを2回受けたところ、テストA、テストBどちらも平均点は50点で明男君の成績はいずれも得点が75点で順位は5番だったとします。このとき明男君の両テストにおける成績評価は同じであるといえるでしょうか。これが必ずしも同じであるとは限らないのです。

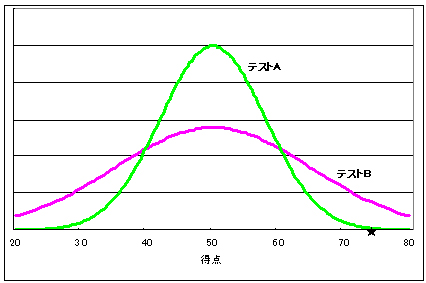
テストAでは全受験生の8割以上が平均点の±10点の範囲に分布している、つまりほとんどの受験生の得点が40～60点というせまい幅のなかにあり、点が詰まっている、あるいは団子状態になっている、それに対してテストBでは全受験生の半分が平均点の±10点のなかに、残り半分はさらにその上下に大きくひらき20～80点と点数の散らばり、分布が広くなっているとします。このように平均点が同じで本人の得点も順位も同じであっても、得点の分布状態が大きく異なれば75点（グラフの★）の価値ないし評価はまったく異なります。明男君の場合でいえばテストAの偏差値のほうがはるかに高くなります。

以上で成績評価に「偏差値」という統計的手法を使うことの意義をご理解いただけたでしょう。なお得点別の人数をグラフで表したとき、平均点をピークにしてほぼ左右対称になっている富士山型（あるいは釣り鐘方）の分布を正規分布といいます。正規分布の場合は「偏差値」は有効ですが、非正規分布の場合、極端な例でいえばふたこぶ状の分布などでは「偏差値」の算出は可能ですが、まったく意味がなくなり判断材料にはなりません。

2.「偏差値」っていろいろある？

上記の例でわかるとおり、同じ生徒でも受験した模試の種類や回の違いによって出てくる「偏差値」の数字がかなり異なることがあります。本人の実力ではなく模試の性格に起因する「偏差値」の変動であれば、その事情を知っておく必要があります。

まず試験問題の難易度の差による場合です。問題が難しくなると点差がつきにくくなり平均点前後に得点が集中し、「偏差値」の上下への広がりの幅が小さくなります。その結果平均点より上では同じ順位でも偏差値は低めになり、平均点より下では同じ順位でも偏差値は高めになります。（平均点から離れるほどこの傾向は強まります。）

特に問題が極度に難しいと平均点が下がるだけでなく分布の山（ピーク）が著しく下位方向に寄って正規分布がくずれ「偏差値」の出方にひずみが生じます。少数の成績最上位の受験生は異様に高い「偏差値」になり、最下位は逆に低い「偏差値」がでにくくなる、つまり「偏差値」が上がるために（見かけ上）成績が上がったように見えてしまいます。

また逆に問題が極度に易しい場合は逆パターンになります。たとえば前回は80点で偏差値70だった。今回は問題がやさしかったので90点以上がたくさんいたため、頑張って満点をとったのに偏差値が67に下がってしまったという笑えない話もありえます。

数年前に高校受験の大手模試で実際にあった例ですが、やや高めの難易度で作問されていた私立高対策模試で、数学が難しすぎて0点続出、英語と国語は易しめで平均点が高かったため。英語20点、国語25点、数学0点だった受験生でなんと数学の「偏差値」が1番高かったという珍事がありました。

次に模試の受験者層の違いによる場合です。次の小話（もちろん架空の話です）を読んでみてください。

―― よし子さんは9月に幅広いレベルの受験生が受けることで知られるC模試を受験したところ、平均点よりちょっと上だったので偏差値53でした。10月には難関校を志望する上位生が多く受けるといわれるD模試を受験したところ「難しくて解けない問題がたくさんあった。」というよし子さんの言葉通り4教科ともひどい点で、偏差値はなんと32でした。お母さんは激怒して「1か月で20以上も下がったじゃないの！あんたのように勉強しない子は、受験（あるいは塾）なんて辞めてしまいなさい！」とよし子さんをしかりつけました。 ――

さて皆さんはこの話を読んでどう思いますか？もうおわかりですね。よし子さんのお母さんの「偏差値」の理解には根本的な誤解があるのです。「偏差値」は各母集団の平均のとき50となります。したがって標準レベルの母集団で偏差値53のよし子さんが、学力上位層の母集団で偏差値32になるのは当然予想されることだったのです。このように大手模試でも受験者層の違いによって「偏差値」が大きく上下するのは当然で、母集団のレベルが全く異なる模試の「偏差値」は尺度の異なる物差しなのです。ですから「偏差値」の推移をみるためには同じ模試を継続的に何回か受けなければいけません。よし子さんは20以上も「偏差値」が下がったとおこられてしまいましたが、とんだ災難だったわけです。

今回は、「偏差値」が母集団のなかでの相対的な位置をあらわす数値であること、また模試の出題レベルによって得点の分布が変われば「偏差値」の出かたも変わり、母集団のレベルが変われば「偏差値」そのものの水準も異なってくる、という話をしてきました。

「偏差値」は学習診断や志望校の合否判定に幅広く使われていますが、「偏差値」の性質を正しく理解していないと、とんでもない判断ミスをしてしまう可能性もあります。保護者の皆さんも「偏差値」についてしっかり理解しておいてください。

次回は「偏差値」による志望校の合否判定についての話を中心にしていく予定です。